路易斯数

Background

定义

路易斯数(Lewis number,Le)的定义是热传导率(thermal diffusion rate)和质量扩散率(mass diffusion rate)的比值： $$ Le=\frac{\alpha}{D}=\frac{\lambda}{\rho D_{im}C_p} $$ where:

• $\lambda$ is the thermal conductivity,
• $\rho$ is the density,
• $D_{im}$ is the mixture-averaged diffusion coefficient,
• $C_p$ is the specific heat capacity at constant pressure.

Le数还可以表示为施密特数Sc和普朗特数Pr的比值 $$ Le=\frac{Sc}{Pr} $$

在甲烷等火焰中，一般认为$Le=1$,

对流扩散方程

热传导$T$: $$ \frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}=\frac{\lambda}{\rho C_p}\frac{\partial ^2 T}{\partial x^2}+\dot{\omega}_T $$

质量扩散$c$: $$ \frac{\partial c}{\partial t}+u\frac{\partial c}{\partial x}=\alpha\frac{\partial ^2 c}{\partial x^2}+\dot{\omega}_c $$

从这两个方程中可以看出，质量扩散和热扩散发生在浓度、温度梯度较大的位置，与梯度的二次方成正比。也就是说热和质的差异扩散主要体现在火焰锋面附近。

Lewis number effect

Le数效应就是传热和传质的差异引起的火焰结构的差异。当Le<1时，火焰的质量扩散大于热扩散率，火焰锋面温度较低，火焰传播速度较慢；当Le>1时，火焰的质量扩散小于热扩散率，火焰锋面温度较高，火焰传播速度较快。当火焰面被拉伸时，火焰面变薄，会加强局部的传热，因此Le<1的火焰的层流火焰速度回变高。对于Le>1的火焰，火焰变薄会增强局部的质量扩散，降低局部的温度，火焰传播速度会变慢。

差异扩散

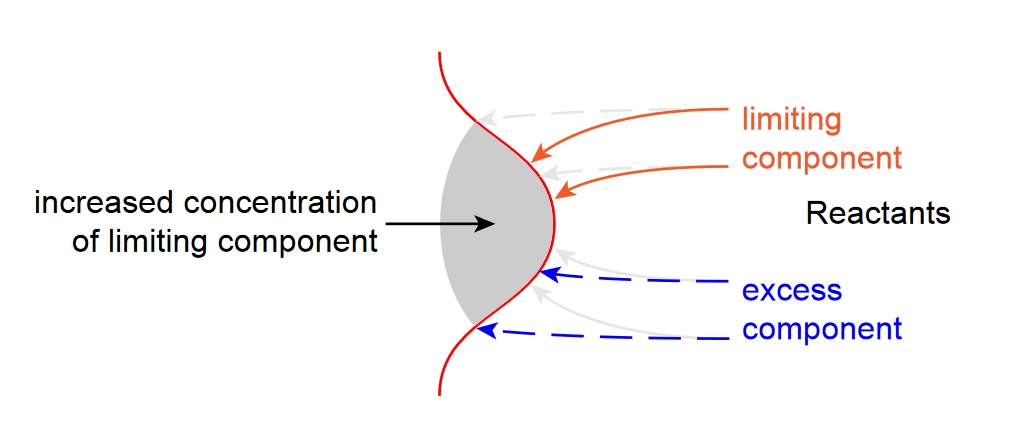
差异扩散是说气态混合物中，不同的物质的扩散模式的差异引起局部的火焰当量比变化，如上图所示。如在贫燃$\rm H_2-AIR$火焰中，在褶皱结构附近的氢气梯度大，且氢气的扩散系数大于氧气、氮气等，容易和空气产生差异扩散现象；另一个例子是在富燃的$\rm n-C_7H_{16}$火焰，火焰面附近的氧气浓度梯度大、且扩散系数大于$\rm n-C_7H_{16}$。

差异扩散是产生热扩散不稳定的基础。

热扩散不稳定

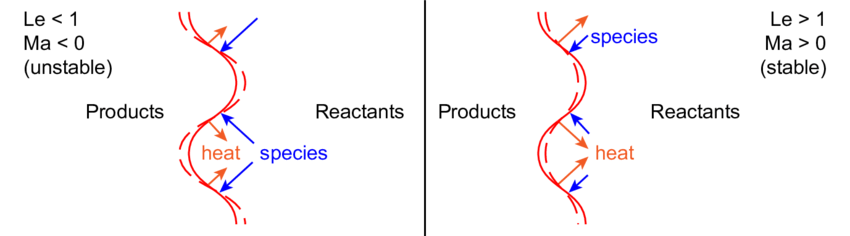
在$Le \ne 1$的火焰中，由于热扩散不稳定的存在，火焰面附近的热传导和质量扩散出现较大的差异性。当Le<1时，质量扩散速率大于热扩散速率，如贫燃的氢气火焰；当Le>1时，质量扩散速率大于热扩散速率，如贫燃的正庚烷火焰。热扩散不稳定( thermo–diffusive instability)是一种本征燃烧不稳定( intrinsic flame instability)，经常发生在Le<1的火焰中，具体表现为出现许多结构较小的褶皱，且褶皱程度随着时间演化越来越大。

热扩散不稳定的机理如下图所示，受到外界扰动的火焰面发生褶皱。当Le<1的时候，在火焰锋面附近，物质扩散速率远大于温度的扩散速率，反应物中的易扩散分子向火焰面附近扩散，物质扩散方向向着浓度梯度最大的方向扩散，因此凸向反应物的区域当量比会更接近1，此时$S_L>S_{L0}$；与此同时，凸向产物区的部分由于反应物在上游被稀释，当量比偏离1，此时$S_L<S_{L0}$。通过以上两个部分的作用，火焰面会变得更加褶皱，因此称为热-质扩散不稳定。 当Le>1的时候，火焰面附近热扩散速率大于物质扩散速率。产物中的热能向火焰面附近扩散，温度扩散方向沿着温度梯度最大的方向扩散，凸向产物区的火焰面收到更多的热量，此时$S_L>S_{L0}$。凸向反应物的火焰面接受的热量更少，火焰面温度较低，此时$S_L<S_{L0}$。通过以上两个部分的作用，褶皱的火焰面会变得平整，因此称为热-质扩散稳定。